Ecuación de la recta

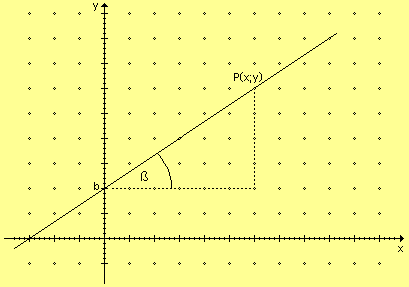
Observando la gráfica de una recta oblicua en un sistema de ejes cartesianos, se distingue que la misma corta al eje de ordenadas ( eje y ) en un punto y forma un ángulo con respecto al eje de abscisas ( eje x ).

El punto donde la recta corta al eje y se denomina ordenada al origen siendo sus coordenadas ( 0; b ). Tomando un punto cualquiera de la recta, distinto de la ordenada al origen, cuyas coordenadas sean ( x; y ) y trazando una recta paralela al eje x que pase por la ordenada al origen y otra recta paralela al eje y que pase por el punto ( x; y ), queda formado un triángulo rectángulo.

Se observa que la recta está inclinada un ángulo ß, con respecto a la recta paralela horizontal.

La longitud del cateto horizontal es x y la longitud del cateto vertical es y - b. Recordando la definición de la tangente trigonométrica de un ángulo

reemplazando en la definición de tangente por las longitudes de los catetos, se obtiene

si se hace   tan ß  =  a,  queda

si se multiplica a ambos miembros por x, y luego se les suma b, el resultado es

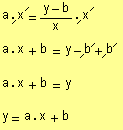
esta última expresión se denomina ecuación de la recta en forma explícita. Se debe tener en cuenta que el coeficiente a se denomina pendiente o coeficiente angular y recordar que el termino b se llama ordenada al origen.

Representación gráfica

Existen dos formas de obtener el gráfico de una recta a través de su ecuación: la primera es a través de una tabla de puntos y la segunda es interpretando los coeficientes de la ecuación. Para todos los ejemplos presentados se utilizarán los dos métodos y por ahora se va a suponer que las rectas están definidas para todo x

observando el valor de la pendiente se tiene que el cateto horizontal ( denominador ) toma valor 5, luego, partiendo de la ordenada al origen, se avanza 5 unidades hacia la derecha ( x > 0 )

desde el punto a que llegamos construimos el cateto vertical, o sea se sube 2 unidades  ( y > 0 )

se puede repetir la construcción anterior, o sea, avanzamos 5 unidades a la derecha y luego 2 unidades hacia arriba

obteniéndose otro punto perteneciente a la recta. Si se unen los puntos obtenidos, queda representada la recta.