| ejercitando |
Radio de Bohr |
Radio de Bohr
De acuerdo al modelo atómico de Bohr, el átomo de hidrógeno consiste en un núcleo relativamente pesado, formado por un protón, que tiene carga eléctrica e positiva, y un electrón, con carga eléctrica -e, orbitando alrededor del núcleo.
Uno de los postulados dice: de todas las órbitas electrónicas, solamente estan permitidas aquellas para las cuales el momento angular del electrón es un múltiplo entero de ħ = h / 2 π .
Simbólicamente el momento angular debe ser
![]()
donde n es un número entero y h la constante de Planck.
Además, el momento angular de una masa m describiendo una órbita circular de radio r es

cumpliendo con la condición de Bohr queda
![]()
donde r n es el radio de la órbita estacionaria correspondiente al número entero n.
Despejando a v de esta última ecuación
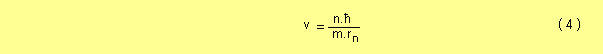
Siendo Z el número atómico del átomo y Z.e la carga eléctrica del núcleo, para cada órbita circular estable, la fuerza de atracción del núcleo debe ser igual a la fuerza necesaria para mantener el movimiento circular, entonces
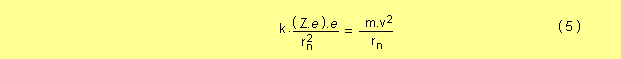
elevando al cuadrado a ambos miembros de la ecuación ( 4 )

despejando v 2 de la ecuación ( 5 )
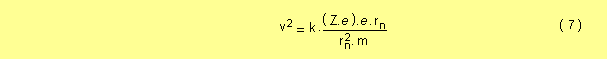
igualando las ecuaciones ( 6 ) y ( 7 )
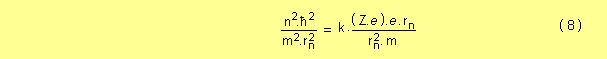
tomando Z = 1, cancelando y despejando el radio queda

Según el modelo de Bohr, los radios calculados por la ecuación ( 9 ) son los únicos posibles para el electrón del átomo de hidrógeno ( recordar que se tomó Z = 1 ). El radio más pequeño corresponde para n = 1 y al valor obtenido se lo denomina radio de Bohr, el cual se representa con el símbolo a0 .
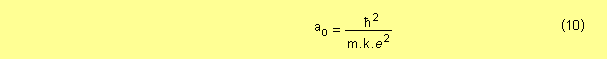
reemplazando por los valores de las constantes, se obtiene

Esta página se
actualizó el 1 de Abril de 2002.
Contactar con ejercitando
para cualquier comentario o error.